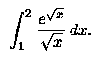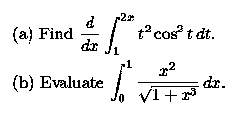Mathematics 140
Sample Exams (taken from the course in previous years)
Partial solutions are available
here. But to make most effective
use of these sample exams, do not consult the answers until you are
done testing yourself.
Caution: This page is still under construction.
Chapter 2
-
Review Worksheet for Chapter 2
The following problems have been taken from Math 140 exams of the last few years.
-
Complete the following definition of a limit.
Let f be a function defined on an open interval containing a,
except possibly at a.
Then L is the limit of f(x) as x approaches
a if ....
-
Using the notation of the above definition, let f(x)
= x2 + 2x + 3, a
= 10 (so that L = 123), and suppose
epsilon = 0.1. Use your calculator to find a delta which satisfies the
condition(s) of the
above definition. Sketch the graph of f on an appropriate
interval to show that your delta works.
-
For the function f below, determine if f is continuous
at a, continuous
from the right at a, or continuous from the left at a, for a
= 0 and a = 1:
f(x) = (sin x) / x for x < 0,
x2 + ex for 0 <= x <= 1,
x + 1 for x > 1.
-
Determine which of the following limits exist. If the limit exists, then
evaluate it. This
is not a calculator problem; you must provide some algebra and
explanation.
- lim as u -> 0 [e3u - e0]/[2u]
- lim as t -> 0 [sqrt t + tan (2 sqrt t]/(sqrt t)
- lim as z -> 0 [1/ ln z]
-
Show that the equation x3 - x = -2
has at least one solution.
This is not a calculator problem, you
must quote the facts you are using and verify that they apply to this problem.
- Now use your calculator to locate all the solutions numerically (to
two decimal places).
Math 140 First Hourly Exam, September 19, 1997
This is a closed book, closed notes 50 minute exam. You may
use your calculator. Do one numbered problem on each of the four answer
sheets. Be sure your name and your TA's name and the problem number
are on each page. Show all your work. If the grader cannot tell how
you obtained an answer you will not receive full credit, even if the answer is
correct.
- a) (5 points) Solve the following
equation for x:
ln (x2-1) - 2 ln (x+1) = ln 2.
b) (5 points) Let l be the line with equation 2x + 4y =
1. Find an equation for
the line perpendicular to l and passing through the point
P = (-1,2).
c) (10 points) Compute the value of sin [pi/3 + pi/4].
- a) (5 points) The height of an
oscillating weight at time t is given by the function
h(t) = et/2 sin(2t).
State the limit you must evaluate in
order to find the vertical velocity of the weight at time t = 0.
b) (10 points) Evaluate this limit.
c) (10 points) Use the Squeezing Theorem to find the limit
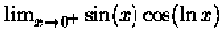 Give your choice for the lower
function f and the upper function
h. What inequalities are you using?
Give your choice for the lower
function f and the upper function
h. What inequalities are you using?
- (30 points) State which of the following limits
exist as numbers or as infinity or -infinity and why. Evaluate those that exist.
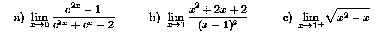
- a) (10 points) State the definition of
what it means
for a function f to be continuous on the closed interval [a,
b].
b) (15 points) In each of the following three intervals [-3, -1],
[-1, 1], and [1, 3]
determine whether or not the Intermediate Value Theorem guarantees the
existence of a
zero of the function f defined by
f(x) = x - 3 + 1 / x. Justify all your answers.
Chapter 3
Math 140 Second Hourly Exam, October 10, 1995
This is a closed book, closed notes 50 minute exam. You will need to
use your calculator. If a problem does not ask you to use
your calculator, we do not expect you to use it in solving the problem.
Do one numbered problem on each of the four answer
sheets. Be sure your name and your TA's name and the problem number
are on each page. Show all your work. If the grader cannot tell how
you obtained an answer you may not receive any credit, even if the answer
is correct.
-
(10 points) Suppose f is a
function differentiable at a value a. Write an equation for the
tangent line to the graph of f at (a, f(a))
in terms of f and f'.
b) (10 points) Approximate the cube root of 28 using differentials.
-
(30 points) Find the derivatives of the following
functions:
(a) (cube root of x) + x cos x
(b) square root of (2 + sin2 x)
(c) (2x) / (1 + 3x).
-
(10 points) Suppose x and y
satisfy exy= y.
Find dy / dx by implicit differentiation.
b) (10 points) Use the Newton-Raphson Method and your calculator
to find an approximate solution for
x3 = 28. Continue until two successive approximations on your
calculator agree.
Use 3 as initial seed value and state the function you use to calculate
the successive approximations. List all the successive approximations
you calculate putting a box
around the last one.
-
(30 points) Joan is holding the string of
a kite. John stands fifteen feet from Joan and releases the kite. It rises vertically into the air. Joan lets out the string at a constant
rate of 10 feet per second. At what rate is the kite rising vertically
when it is twenty feet off the ground?
-
Review Worksheet for Chapter 3
The following problems have been taken from Math 140 exams of the last few years.
-
a. Let f(x) = x / (x+1).
Use the definition of the derivative as a limit to find f'(1).
b. Let f(x) = x2 + sin x - 1.
Use the Newton-Raphson method and your calculator to
approximate a solution in (0, 1) of f(x) = 0.
Continue until the output of your
calculator does not change. Write down your initial value and the final
output of the calculator.
c. Let g(x) = x3 - x - 2.
Using the seed value x1 = 1 in the Newton-Raphson method, find the next
two approximates x2 and x3 for a root of g(x).
-
a. In the following, find f'(x).
(i) f(x) = (tan x) / (-3 + sqrt x)
(ii) f(x) = (3x - 2 sin x)5/2.
b. Suppose y is a function of x that satisfies
x5 cos y + 3x - y2 = 1.
Find dy / dx.
c. Let f(x) = x sec x. Find f''(x).
-
a. Let f(x) = x - 1 / x.
Find an equation of the line tangent
to the graph of f at (1, 0).
b. A right triangle whose two legs always have the same length is growing in size.
Its area is increasing at a rate of 100 square miles per year. How fast is the length of
the hypotenuse of the triangle increasing when the area is sqrt 2 square miles?
c. Water is leaking onto a floor from a dripping faucet.
The water is forming a semi-circular
puddle next to a wall.
The puddle is growing in surface area at a rate of 10 square inches
per minute. How rapidly is the radius of the puddle growing at the moment
when the area of the puddle is 50 pi square inches?
Chapter 4
Chapter 5
The Whole Course
-
Final Exam, May 1997
- Find the derivatives of
- tan (3x) / (1 + x3).
- ln ( sin (x2 + x + 1)).
- Find an equation of the line tangent to the graph of
x4 + y4 = 17 at the point (2,1).
- Compute the indicated limits:
- limit as x goes to 0 of (x / tan (19x)).
- limit as x goes to infinity of
((3x2 + 5) / (4x2 - x + 1)) +
((sin x) / x )
- Assume that the half-life of radium is 1590 years. How long will it
take for 99% of a sample of 100 grams to disappear?
-
- Show that the equation x5 + 1
= x2 + 4 has a solution
which lies between 0 and 2. Carefully explain how this follows from the appropriate
theorem.
- Use Newton's Method to estimate this solution to as many places as your
calculator allows. Specify your first guess and the first iterate as well
as the final answer.
- A cylindrical barrel (with a circular base) is to contain 32 cubic meters.
Suppose that material for the side costs $1 per square meter and the
(different) material for the top and bottom costs $2 per square meter.
Find the dimensions of the barrel for which the cost of the material is least.
- Let f (x) = (x - 3) / (x - 2)2. You
may assume that
f' (x) = (4 - x) / (x - 2)3,
f'' (x) = 2 (x - 5) / (x - 2)4.
- Determine the intervals on which f is increasing, and the
intervals on which f is decreasing.
- Determine all relative extreme values of f, and where they occur.
- Determine the intervals on which f is concave downward, and the
intervals on which f is concave upward.
- Find all inflection points of f.
- Determine all asymptotes of f.
- Carefully sketch the graph of f, incorporating the information
from above. Note: you may use your calculator here, but no credit
will be given for a sketch without the requested discussion.
-
- Let f (x) = x2.
Using the definition of the
derivative as a limit, prove that f' (10) = 20.
- Let f (x) = 1 - x4. Compute the upper sum
for the partition P = {-2, -1, 1, 3} of the interval [-2, 3].
- Evaluate:
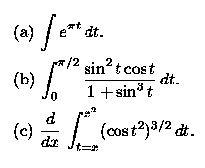
- Find the area of the region bounded by the graphs of y = 3x
and y = x3 - x.
-
Final Exam, December 1997
- Determine whether each limit exists as a real number as infinity or
-infinity, or fails to exist. If the limit exists, evaluate it. Give reasons
for your answers.
- limit as x goes to infinity of (sqrt (1 + 9x2) /
x).
- limit as h goes to 0 of (sin ((pi/6) + h) - (1/2)) / h.
- limit as x goes to 1 of f (x), where
f (1) = 0, f (x) = 2x - 6 for x < 1,
f (x) = -(x + 1)2 for x > 1.
- In each case find f' (x).
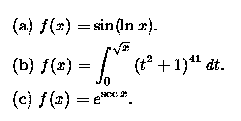
- If f (x) = sqrt (x), find f' (4) directly
from the definition of the derivative as a limit.
- Find an equation of the line tangent to the graph of the equation
x2 + x2y2
+ y3 = 13 at the point (1,2).
- Explain why x3 + x - 7 = 0
for at least one value
x > 0.
- Explain why x3 + x - 7 = 0
for at most one value
x > 0.
- Approximate the value x > 0 with x3 + x - 7 = 0
using the bisection method. Choose the two initial values
to be whole numbers and continue until your approximation is within 1/8 of the
actual value of x. Show all steps of your calculation.
- Find the minimum length of a line segment connecting the point (1,0)
to the ellipse given by (x2 / 20) +
(y2 / 15) = 1.
Clearly identify the function you are minimizing and the methods
you use to find its maximum.
- Let f (x) = x2 - 8 ln (x2 + 3)
for all x. Note:
f' (x) = 2x - (16 x / x2 + 3)
and
f'' (x) = 2 (x4 + 14x2 - 14)
/ (x2 + 3)2.
- What kinds of symmetry, if any, does the graph of f have?
- Find the exact values of all critical numbers of the function f.
- Determine if f has a relative maximum value, relative
minimum value, or neither at each of these critical numbers. Be sure to
explain why.
- Determine the exact value of the x and y coordinates
of each inflection point of f.
- A function f is decreasing on [0,2] and increasing on [2,4].
the partition P consists of the points
{0, 1/2, 1, 3/2, 2, 5/2, 3, 7/2, 4}. A table of values of f
is given below.
| x |
0 | 1/2 | 1 | 3/2 | 2 |
5/2 | 3 | 7/2 | 4 |
| f (x) | 8 | 6 |
5 | 2 | 1 |
2 | 4 | 9 | 10 |
- Sketch the graph of such a function f defined on [0,4]
with these values.
- Find the left sum for the function f and the partition P.
- Find the lower sum for the function f and the partition
P.
- A person is flying a kite. The kite is moving with the wind
horizontally above the ground at a height of 300 feet. When 500 feet of
string have been let out, the kite is pulling string out at a rate
of 20 feet per second. Find the wind velocity.
- Find the exact value of:
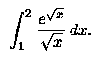
- Let f (x) = x3 + x2
- 2x - 1
and g (x) = x3 - 1.
Find the area A of the bounded
region between the graphs of f and g.
-
Final Exam, December 1992
- Find the derivative of the given function:
- f (x) = (sin 3x) / (1 + x2).
- g (x) = x ln (1 + x2).
- Find an equation of the line tangent to the graph of
x - y2 = 2x2 - 4y
at the point (-1,1).
-
- Evaluate the limit as x -> -3 of (x2 - 9)
/ (x + 3).
- Evaluate the limit as x -> 0 of (tan 3x) / (2x).
- Using the known inequality
u2 - (u4 / 2)
<= ln (1 + u2) <= u2 for
0 < |u| < 1,
evaluate the limit as u -> 0 of (ln (1 + u2) /
u2). Explain your solution.
- Sand falling at the rate of 2 cubic inches per second forms a conical
pile so that the radius of the base of the cone always equals twice the
height of the cone. Find the rate at which the radius is changing at
the instant the height is 6 inches. (The volume of a cone with base
radius r and height h is pi r2h / 3.)
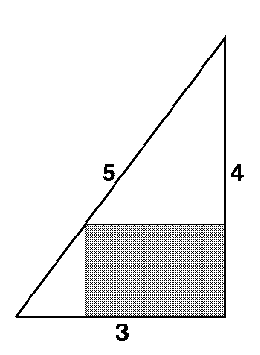
- Find the maximum area of a rectangle inscribed in a 3-4-5 right triangle
as in the diagram. Check that your answer is the maximum area.
- For the first few seconds of a car race, the distance a car has
traveled is given by f(t) =
t2et (feet). Find the velocity of the car
after 2 seconds.
- Suppose g is a function with second derivative
g''(x) =
x3(x - 1)2(x - 2)5.
Find the values of c such that (c, g(c))
is an inflection point of the graph of g.
- Let f(x) = x2 ln x.
- Find the critical point(s) of f.
- For each critical point c you found in part (1), determine
whether f has a relative maximum, a relative minimum, or
neither at c. Explain your answer.
- Does f have either a global maximum or a global minimum
value on (0, infinity)? Justify your answer.
-
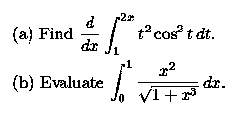
- Find the area A of the bounded region between the graphs of
y = 2x and y = 2x2 - 4x + 4.
As part of your solution, indicate clearly which graph forms the
upper boundary of the region.
- For the last problem you have a choice. Do one or the other
of the two parts, but not both. Only one part will be graded.
- If you plot y = x4 - 3x3
+ x - 7 on your calculator, you will see that there are two
roots of the equation x4 - 3x3
+ x - 7 = 0. Use the Newton-Raphson method, starting with
an initial guess obtained from your graph, to approximate the
larger root. Continue to apply the Newton-Raphson method until the
calculator's output no longer changes. Write down only your initial
guess and the final answer.
- Using the known inequality 2x4 <=
x4(4 + 5x3)1/2 <=
3x4 for 0 <= x <= 1, find positive
upper and lower bounds for the integral from 0 to 1 of
x4(4 + 5x3)1/2. Show your work.
Do not attempt to evaluate the integral exactly.